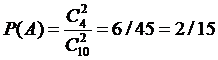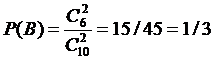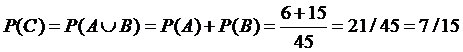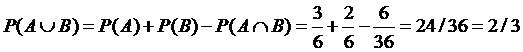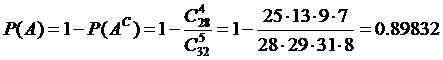Below are some solved simple exercises and applications:

1)  Find the probability of getting a multiple of 2 at a die roll.
Solution: The number of outcomes that are favorable to respective event is three (these are: {2}, {4}, {6}).  The number of equally possible outcomes is six, so the probability is 3/6 = 1/2 = 50%.

 2)  There are three pairs of socks of different colors in a basket. Two socks are randomly extracted from the basket. What is the probability of getting two socks of same color? 
Solution:  The number of equally possible cases is the number of all 2-size combinations of socks, namely, C(6, 2) = 15. The number of favorable cases is three, because we have three pairs of socks having the same color. Thus, the probability is  3/15 = 1/5 = 20%.

3)  An urn contains four white balls and six black balls. Two balls are drawn simultaneously. Find the probability of the events: a)  A – drawing two white balls;  b)  B – drawing two black balls;  c)  C – drawing two balls of the same color.
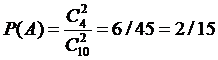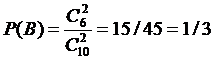Solution: The number of possible cases is C(10, 2). a)  The number of cases that are favorable to event A is C(4, 2); therefore,. b)  Similarly, . c)  We have 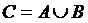. The events A and B are incompatible, so .

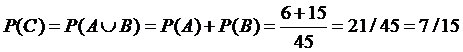4)  Two dice, one red and one blue, are rolled. Consider the events: A – occurrence of a number less than 4 on the red die;  B – occurrence of a number less than 3 on the blue die. Find P(A or B).
Solution:  The cases that are favorable to A are {1}, {2} and {3}; therefore, P(A) = 3/6. The cases that are favorable to B are {1} and {2}; therefore, P(B) = 2/6. The cases that are favorable to A and B correspond to the ordered pairs (1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2), totalling six, in a probability field where the number of equally possible cases is 6 x 6 = 36. We then have P(A and B) = 6/36. The requested probability is.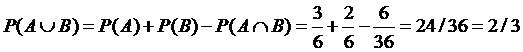

5)  At a blackjack game, calculate the probability for a player to get a total of twenty points from the first two cards (provided no other cards are shown), if a 52-card deck is used. 
Solution:  The variants totaling twenty points are of the type A + 9 or 10 + 10 (as a value; that is, any 2-size combination of cards from 10, J, Q, K). We have sixteen variants A + 9 (4 aces and 4 nines) and C(16, 2) = 120 variants 10 + 10 (all 2-size combinations of cards from the sixteen cards with a value of 10). The number of all possible distribution variants for two cards is C(52, 2)=1326. The probability is then P = (16 + 120)/1326 = 68/663.

6)  We have two urns, the first containing three white balls and four black balls and the second three white balls and five black balls. A ball is drawn from a randomly chosen urn. Find the probability for the drawn ball to be white. 
Solution:  Denote the events: A – the first urn is the chosen one; B – the second urn is the chosen one; C – the drawn ball is white. A and B form a complete system of events and P(A) = P(B) = 1/2. We have  P(C│A) = 3/7 and  P(C│B) = 3/8.  According to total probability formula, we have: P(C) = P(A)P(C│A) + P(B)P(C│B) = (1/2) x (3/7) + (1/2) x (3/8) = 45/112 = 0.40178.

7)  Five cards are drawn at once from a 32-card deck, containing cards from 7's up to aces. What is the probability of the five cards containing at least one queen (Q)?
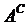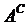Solution:  Denoting by A the event to be measured the five extracted cards contain at least one Q, we then calculate the probability of the contrary event – the five extracted cards contain no Q.The equally possible elementary events are the occurrences of 5-size combinations of cards from the 32, a total of C(32, 5). The combinations that are favorable to event  have the form (xyztv), with x, y, z, t, v taking any card as value, except the four Q-cards. They total C(32 – 4, 5) = C(28, 5). We then have: .

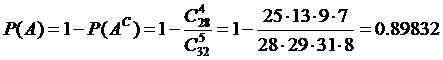For a broad range of applications in gambling, see the gambling section.

Author

The author of this page is Catalin Barboianu (PhD). Catalin is a games mathematician and problem gambling researcher, science writer and consultant for the mathematical aspects of gambling for the gaming industry and problem-gambling institutions. Profiles:   Linkedin   Google Scholar   Researchgate