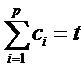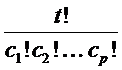|
There is a wide variety of the slot machines with
regard to parametric design and rules. The configuration of a slot
machine is specified by the configuration of its display and the
configuration of its reels.
Configuration of the display
The display of a slot
machine shows the outcomes of the reels in groups of spots (spot
refers to a unit part of a reel holding one symbol, visible
through its window; a spot on the display corresponds to a stop
of the reel; a window can show one or more spots) having a certain shape
and arrangement. The configuration of the display can be defined and
modeled mathematically through a Cartesian grid of integers, where the
gridʼs points stand for the reel spots/stops and a (pay)line is a finite
set of minimum 3 points that can be connected through a path linking
successively neighboring points of that set. The length of a line is the
cardinality of that set. Most of the slot machines have the display
arranged as a rectangular grid. Lines can be of any shape and complexity
and have all kinds of geometrical and topological properties. There are
horizontal, vertical, oblique, or broken lines; symmetric, transversal
lines; triangular, trapezoidal, zigzag, stair, or double-stair lines.
|

Horizontal, vertical, oblique,
and broken lines
|

Triangular line |

Trapezoidal line
|
|

Zigzag lines
|

Double-stair line
|

Symmetric upper-lower
transversal triangular line |
The paylines of slot machines can be of any
complexity for each slot machine in part, but usually they have
particular shapes, following properties such as non-self crossing,
colinearity, symmetry, up-down or left-right direction, and/or crossing
over the reels.
With respect to probability calculus, there are
only the length of a line and the number of particular lines in a given
rectangular grid (for complex events involving several paylines) that
count, regardless of other properties of them. For instance, the number
of horizontal lines included in an m
x n-size rectangular grid (m rows and
n columns) is given in the next table.
Table of values
for the number of horizontal lines in a rectangular grid
|
n
m |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
0 |
2 |
6 |
12 |
20 |
30 |
42 |
56 |
|
3 |
0 |
3 |
9 |
18 |
30 |
45 |
63 |
84 |
|
4 |
0 |
4 |
12 |
24 |
40 |
60 |
84 |
112 |
|
5 |
0 |
5 |
15 |
30 |
50 |
75 |
105 |
140 |
|
6 |
0 |
6 |
18 |
36 |
60 |
90 |
126 |
168 |
|
7 |
0 |
7 |
21 |
42 |
70 |
105 |
147 |
196 |
|
8 |
0 |
8 |
24 |
48 |
80 |
120 |
168 |
224 |
|
9 |
0 |
9 |
27 |
54 |
90 |
135 |
189 |
252 |
The number of transversal oblique lines included in
an m x n-size rectangular grid is given in the next
table.
Table of values
for the number of transversal oblique lines in a rectangular grid
|
n
m |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
4 |
0 |
4 |
2 |
4 |
6 |
8 |
10 |
12 |
|
5 |
0 |
6 |
4 |
2 |
4 |
6 |
8 |
10 |
|
6 |
0 |
8 |
6 |
4 |
2 |
4 |
6 |
8 |
|
7 |
0 |
10 |
8 |
6 |
4 |
2 |
4 |
6 |
|
8 |
0 |
12 |
10 |
8 |
6 |
4 |
2 |
4 |
|
9 |
0 |
14 |
12 |
10 |
8 |
6 |
4 |
2 |
The number of left-right transversal trapezoidal
lines included in an m x n-size rectangular grid is given
in the next table.
Table of values
for the total number of left-right transversal trapezoidal lines in a
rectangular grid
|
n
m |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
2 |
|
3 |
0 |
0 |
4 |
4 |
6 |
6 |
6 |
6 |
|
4 |
0 |
0 |
6 |
6 |
10 |
10 |
12 |
12 |
|
5 |
0 |
0 |
8 |
8 |
14 |
14 |
18 |
18 |
|
6 |
0 |
0 |
10 |
10 |
18 |
18 |
24 |
24 |
|
7 |
0 |
0 |
12 |
12 |
22 |
22 |
30 |
30 |
|
8 |
0 |
0 |
14 |
14 |
26 |
26 |
36 |
36 |
|
9 |
0 |
0 |
16 |
16 |
30 |
30 |
42 |
42 |
Configuration of the
reels
Distribution of the symbols
Each symbol appears a number of times on the reel.
Together, they fill all stops of the reel – that is, the number of stops
is the sum of the numbers of instances each distinct symbol appears on
the reel (if the reel has blanks, this statement also holds, as we can
consider the blank as a new symbol).
Denote by t the number of stops and by p
the number of distinct symbols
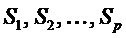 on
the reel. Denote by on
the reel. Denote by 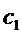 the
number of symbols the
number of symbols 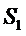 ,
by ,
by 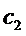 the
number of symbols the
number of symbols 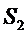 ,
and so on, by ,
and so on, by 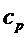 the
number of symbols the
number of symbols 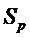 .
Obviously, .
Obviously, 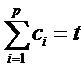 and and
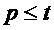 . .
Definition: Call the vector
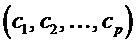 the
distribution of the symbols the
distribution of the symbols
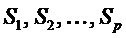 on
the reel. on
the reel.
The distribution of the symbols tells us how many
of each symbol is on the reel. Each reel has its own distribution of
symbols.
There are
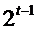 possible
distributions of symbols on a t-stops
reel, for all possible values of p. possible
distributions of symbols on a t-stops
reel, for all possible values of p.
Common symbols
on the reels
Definition: Let
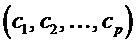 be
a distribution of the p symbols on the t stops of a reel.
Call arrangement of the symbols on the reel any function a
from the set of stops to the set of distinct symbols, such that be
a distribution of the p symbols on the t stops of a reel.
Call arrangement of the symbols on the reel any function a
from the set of stops to the set of distinct symbols, such that
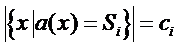 for
any i from 1 to p (that is, the number of stops having
assigned symbol for
any i from 1 to p (that is, the number of stops having
assigned symbol 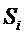 by
function a is by
function a is 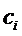 ). ).
The number of possible arrangements of the symbols
on a reel in a given distribution is
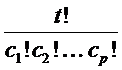 . .
The arrangement of symbols on the reel does not
count toward probability estimations, except for events related to
paylines that contain stops of the same reel or complex events related
to such non-independent paylines. In other words, for estimating odds,
usually we do not need to know how the symbols are arranged on the reel,
but how many instances of each symbol we have on the reel and their
total number (the number of stops).
There are two types of slot machines with respect
to the symbol distributions on the reels:
A – All reels have the same distribution of
symbols; each symbol S has the same distribution on the t
stops of each reel, denoted by
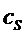 ; ;
B
– The reels have different numbers of stops
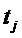 and
each symbol S has different distributions on the stops of the
n reels, denoted by: and
each symbol S has different distributions on the stops of the
n reels, denoted by: 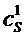 on
reel 1, on
reel 1, 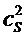 on
reel 2, ..., on
reel 2, ..., 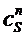 on
reel n. on
reel n.
All probability models and computations should be worked
out assuming one of the two cases A and B.
back to slots index
|
Author |
|
The author of this page is Catalin Barboianu
(PhD). Catalin is a games mathematician and problem gambling researcher,
science writer and consultant for the mathematical aspects of gambling
for the gaming industry and problem-gambling institutions.
Profiles:
Linkedin
Google Scholar
Researchgate |
 |
|